Introducción a los Métodos Semiempíricos
Ya hemos visto que existen diferentes niveles de teoría para estudiar
sistemas químicos. La mecánica molecular supone un
modelo de palitos y bolitas. El modelo de palitos y bolitas supone
que las distribuciones electrónicas son fijas y aditivas.
Por lo tanto, la mecánica molecular comienza a tener problemas a
la hora de modelar sistemas conjugados extendidos. Aumentar el nivel
de teoría implica calcular distribuciones electrónicas.
Los métodos semiempíricos constituyen el segundo nivel de
teoría que utilizaremos en este curso. Como su nombre lo dice
("semi-empírico"), estos métodos contienen una parte basada
en teoría y una parte basada en datos obtenidos experimentalmente.
La simplificación introducida en el nivel semiempírico consiste
en suponer que el comportamiento químico depende exclusivamente
de la capa de valencia.
El Hamiltoniano como descripción de la energía de un sistema
Así como la mecánica molecular tiene su base en los tipos
de átomos y el campo de potenciales, el fundamento de los métodos
semiempíricos es el llamado "Hamiltoniano". Brevemente, un
hamiltoniano es una descripción de la energía de un grupo
de partículas. Supongamos que tenemos dos partículas
con la misma masa, el mismo radio y la misma carga. La función
que describe cómo interactúan es la ley de Coulomb.
Dependiendo de si las cargas tienen signos iguales u opuestos, mediante
la ley de Coulomb podemos calcular la energía necesaria para mantener
las partículas en una configuración determinada. En
este caso, podemos considerar a la ley de Coulomb como un hamiltoniano.
En general, el problema principal de los cálculos en
química cuántica, consiste en calcular el comportamiento
de unos electrones cuando están atrapados en el campo eléctrico
de unos núcleos fijos. Otro modo de decirlo es que queremos
calcular la estructura electrónica de la molécula.
Aquí cabe hacer una distinción: la mecánica molecular
no trata de calcular la distribución electrónica, sino que
supone que es posible partir una distribución electrónica
y luego sumar los pedacitos de diferentes moléculas. Entonces
lo que nos interesa es calcular cosas como el comportamiento conformacional
de la molécula (los núcleos no están fijos).
En el caso de los métodos mecano-cuánticos, como los semiempíricos
y ab initio, tenemos que calcular la distribución electrónica
y para esto es necesario suponer que los núcleos están fijos
(examinamos una sola conformación). Por supuesto que podemos
calcular comportamiento conformacional con métodos mecano-cuánticos,
pero esto alarga mucho los cálculos porque para cada conformación
hay que recalcular la estructura electrónica. Dicho sea de
paso, en esto consiste una buena parte del poder de los métodos
mecano-cuánticos.
El Traslape Diferencial
En los cálculos de estructura electrónica utilizamos un concepto
poco intuitivo que explica buena parte de la complejidad de los cálculos:
el traslape diferencial. El traslape entre dos átomos está
constituido por aquella región del espacio a través de la
cual comparten densidad electrónica. Intuitivamente podemos
identificar las zonas de traslape con las "rayitas" que dibujamos en las
estructuras de Lewis y con las cuales simbolizamos un par de electrones.
Sin embargo, el traslape entre los átomos de una molécula
no está limitado a la interacción entre pares de átomos.
Desde los cursos de licenciatura sabemos que cuando combinamos dos orbitales
atómicos obtenemos dos orbitales moleculares. Lo que no es
tan obvio, es que los orbitales moleculares son propios de toda la molécula,
es decir, no podemos decir que, p. ej., un orbital de un C y uno de un
H forman el orbital correspondiente a un enlace C-H. Ese par de orbitales
está disperso sobre todos los núcleos de la molécula,
lo cual significa que cada átomo interactúa uno-a-uno con
todos los demás. Puesto de modo más sencillo: en el
caso general, cuando tomamos un número n de orbitales atómicos,
obtendremos un número n de orbitales moleculares y todos
los orbitales atómicos participan en la formación de cada
orbital molecular. Al traslape con átomos más lejanos
(1-3, 1-4, . . .) que los vecinos inmediatos (1-2) le llamamos traslape
diferencial.
Afortunadamente, en muchas ocasiones podemos olvidarnos del traslape
diferencial (dado que su magnitud tiende a ser pequeña), o sustituir
su cálculo con algunas constantes, lo cual simplifica mucho los
cálculos.
Dentro de los métodos semiempíricos, existen varias aproximaciones
para calcular la estructura electrónica de una molécula.
El más antiguo es el llamado Complete Neglect of Differential Overlap,
CNDO (Desprecio Completo del Traslape Diferencial). Como su nombre
lo dice, este método supone que el traslape diferencial siempre
vale cero. Posteriormente surgió otro esquema llamado Intermediate
Neglect of Differential Overlap (INDO), el cual toma en cuenta interacciones
con átomos un poco más lejanos. Prácticamente
todos los Hamiltonianos en uso son perfeccionamientos de INDO, algunos
ajustados para aplicaciones muy específicas, p. ej., ZINDO, desarrollado
por Michael Zerner, es un hamiltoniano especial para cálculos de
cantidades espectroscópicas. También está
MINDO (Modified Intermediate Neglect of Differential Overlap) en sus versiones
MINDO, MINDO-2 y MINDO-3 (todas las cuales están ya obsoletas).
MNDO (Moderate Neglect of Differential Overlap) proveyó un perfeccionamiento
significativo sobre INDO y a partir de MNDO han surgido AM1 (Austin Model
1) y PM3 (Parametrization Method 3). Estos tres últimos (MNDO,
AM1 y PM3) todavía tienen amplia utilización en química
computacional. ZINDO es muy utilizado para su nicho particular.
Ejercicios de entrenamiento con MOPAC
Estructura de una matriz-Z
Una matriz-Z es un formato para describir una estructura molecular.
El formato es bastante intuitivo. Consiste en diez columnas divididas
del siguiente modo: una para símbolos químicos de los elementos
involucrados, tres para las llamadas "coordenadas internas" (longitudes
de enlace, ángulos de enlace y ángulos de torsión),
tres para la tabla de conectividades y tres más para especificar
los grados de libertad (etiquetas que indican si un grado de libertad es
optimizable o no). Veamos un ejemplo, matriz-Z para la anilina:
N 0.00000 0 0.00000 0 0.00000 0 0 0 0
C 1.39980 1 0.00000 0 0.00000 0 1 0 0
C 1.41479 1 120.73248 1 0.00000 0 2 1 0
C 1.39015 1 120.37746 1 184.52896 1 3 2 1
C 1.39397 1 120.65777 1 359.56372 1 4 3 2
C 1.39408 1 119.48771 1 0.09823 1 5 4 3
C 1.38995 1 120.78687 1 359.91238 1 6 5 4
H 1.09994 1 119.59724 1 179.82098 1 7 6 5
H 1.10058 1 119.82602 1 179.98697 1 6 5 4
H 1.09855 1 120.26965 1 180.07834 1 5 4 3
H 1.10041 1 119.44460 1 179.63330 1 4 3 2
H 1.10001 1 120.08910 1 3.89183 1 3 2 1
H 0.99585 1 114.21112 1 334.29825 1 1 2 3
H 0.99595 1 114.22128 1 201.88809 1 1 2 3
Para entender mejor el formato, es mejor ver la función de
cada columna en un orden diferente al consecutivo.
a) La primera columna muestra los símbolos atómicos para
cada átomo que forma la molécula de anilina.
b) Las últimas tres columnas forman la tabla de conectividades.
¿Qué es la tabla de conectividades? Es una lista que
nos dice en qué orden están enlazados los átomos,
identificados por el orden según el cual aparecen en la matriz-Z.
En la octava columna vemos que el nitrógeno es el átomo 1,
un carbono el número 2 y así hasta llegar al hidrógeno
número 14. Los átomos están numerados como lo
muestra la figura:
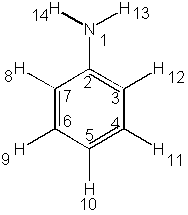c) La segunda columna forma parte del grupo de coordenadas internas: son
las longitudes de enlace en angstroms. Utilizando esta columna junto
con la primera de la tabla de conectividades, vemos que el átomo
2 está a una distancia de 1.39980 Å del átomo 1 y así
sucesivamente.
d) La tercera columna (que está formada por casi puros "1"s)
especifica si un grado de libertad dado está disponible para su
optimación. En este caso vemos que todas las longitudes de
enlace (excepto las que tienen valor de 0.00) están disponibles
dado que el valor de la etiqueta correspondiente es "1". Si prefiriéramos
que MOPAC dejara una longitud de enlace "congelada", pondríamos
un valor de "0" en lugar del "1" y entonces MOPAC variaría todos
las demás coordenadas internas, menos esa.
e) La octava y la novena columnas (primera y segunda de la tabla de
conectividades) especifican cuáles átomos forman un ángulo.
Vemos que el átomo númeo 3 (que está a una distancia
de 1.41479 Å del átomo 2), forma un ángulo de 120.73248°
con los átomos 2 y 1. Esto es, el ángulo N1-C2-C3 es
igual a 120.73248°.
f) La cuarta columna indica los valores de los ángulos especificados
por la tabla de conectividades.
g) La quinta columna (nada que ver con la de la Segunda Guerra Mundial)
tiene la misma función que la tercera: decir si un ángulo
dado es verdaderamente libre para su optimación.
h) Tomando juntas las columnas octava, novena y décima, sabemos
cuáles átomos forman una torsión (también llamado
un ángulo diedro). Por ejemplo, el átomo 4 forma una
torsión con los átomos 3, 2, y 1. Para poder definir
una torsión no es necesario que el enlace tenga rotación
libre, basta que sean cuatro átomos enlazados consecutivamente.
i) La sexta columna nos da los valores de las torsiones dadas por la
tabla de conectividades. En el caso del átomo 4, vemos que
su ángulo de torsión con respecto al átomo 1 (a través
de los átomos 3 y 2) es de 184.52896°.
A este sistema de descripción de la estructura le llamamos "coordenadas
internas", porque los ejes del sistema de coordenadas surgen de las posiciones
de los átomos de la molécula. También vemos
que las coordenadas internas constituyen un sistema "no-redundante": contienen
la información mínima necesaria y suficiente para describir
completamente y sin ambigüedades una estructura molecular. Tienen
además la ventaja de su más fácil comprensión
por humanos (a la computadora le es indiferente si le alimentamos coordenadas
internas, coordenadas internas redundantes o coordenadas XYZ).
Análisis conformacional de moléculas sencillas: etano y butano
Utilice MOLGEN para convertir estructuras óptimas de etano y butano
(obtenidas por MOLGEN) a archivo de entrada de MOPAC (INPUT FILE).
Para convertir a archivo de entrada de MOPAC: abra MOLGEN, vaya a INTERFACES
y seleccione AMPAC/MOPAC y seleccione MOPAC. Elija WRITE INPUT FILE.
El archivo generado tendrá extensión .mop. Abra el
archivo con Wordpad y cambie manualmente los números atómicos
por símbolos (el "99" al final no es un número atómico).
Emplee los Hamiltonianos AM1 y PM3 para evaluar la diferencia de energía
entre las formas eclipsada y alternada en ambas moléculas.
Además, efectúe una coordenada de reacción para la
rotación del etano alrededor del enlace C-C y otra para el butano
alrededor del enlace C2-C3. Para las instrucciones acerca de cómo
correr una coordenada de reacción ("reaction path"), consulte el
manual de MOPAC.
Análisis conformacional de anillos: ciclohexano silla y bote torcido
Calcule los calores de formación del ciclohexano silla y el ciclohexano
bote torcido utilizando los hamiltonianos AM1 y PM3 y compare los resultados
contra aquellos obtenidos por MOLGEN y por vía experimental.
Esta página ha sido visitada:
veces